Блочное умножение матриц для программистов

Ребята, сегодня я узнал об очень интересном способе перемножения матриц и спешу поделиться с вами. Как известно, матрицы умножаются друг на друга строка на столбец или столбец на строку. Формула поэлементного умножения матриц размерностью 2 на 2 выглядит вот так:

$\begin{bmatrix}A_{11}&A_{12} \\A_{21}&A_{22}\end{bmatrix}\begin{bmatrix}B_{11}&B_{12}\\B_{21}&B_{22}\end{bmatrix}=\begin{bmatrix}C_{11}&C_{12} \\C_{21}&B_{22}\end{bmatrix}$ ,

где
$\begin{bmatrix}C_{11}&C_{12} \\C_{21}&B_{22}\end{bmatrix}=\begin{bmatrix}A_{11}*B_{11}+A_{12}*B_{21}&A_{11}*B_{12}+A_{12}*B_{22} \\A_{21}*B_{11}+A_{22}*B_{21}&A_{21}*B_{12}+A_{22}*B_{22}\end{bmatrix}$

Оказывается, с помощью этой же формулы можно рекурсивно разложить умножение больших матриц. Возьмем для примера умножение двух матриц 4×4:

$\begin{bmatrix}a_{11}&a_{12}&a_{13}&a_{14}\\a_{21}&a_{22}&a_{23}&a_{24}\\a_{31}&a_{32}&a_{33}&a_{34}\\a_{41}&a_{42}&a_{43}&a_{44}\end{bmatrix}\begin{bmatrix}b_{11}&b_{12}&b_{13}&b_{14}\\b_{21}&b_{22}&b_{23}&b_{24}\\b_{31}&b_{32}&b_{33}&b_{34}\\b_{41}&b_{42}&b_{43}&b_{44}\end{bmatrix}=\begin{bmatrix}c_{11}&c_{12}&c_{13}&c_{14}\\c_{21}&c_{22}&c_{23}&c_{24}\\c_{31}&c_{32}&c_{33}&c_{34}\\c_{41}&c_{42}&c_{43}&c_{44}\end{bmatrix}$

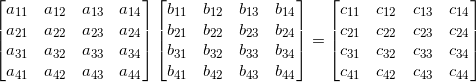
Каждую матрицу можно разбить на блоки 2×2. По четыре блока на каждую:

$\begin{array}{|cc|cc|}a_{11}&a_{12}&a_{13}&a_{14}\\a_{21}&a_{22}&a_{23}&a_{24}\\\hline a_{31}&a_{32}&a_{33}&a_{34}\\a_{41}&a_{42}&a_{43}&a_{44}\end{array}\ \ \ \begin{array}{|cc|cc|}b_{11}&b_{12}&b_{13}&b_{14}\\b_{21}&b_{22}&b_{23}&b_{24}\\\hline b_{31}&b_{32}&b_{33}&b_{34}\\b_{41}&b_{42}&b_{43}&b_{44}\end{array}\ \ \ \begin{array}{|cc|cc|}c_{11}&c_{12}&c_{13}&c_{14}\\c_{21}&c_{22}&c_{23}&c_{24}\\\hline c_{31}&c_{32}&c_{33}&c_{34}\\c_{41}&c_{42}&c_{43}&c_{44}\end{array}$

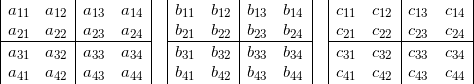
Затем эти блоки можно умножить по формуле, приведенной в начале.

Пример для первого блока:

$C_{11}=\begin{bmatrix}c_{11}&c_{12}\\c_{21}&c_{22}\end{bmatrix}=\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix}\begin{bmatrix}b_{11}&b_{12}\\b_{21}&b_{22}\end{bmatrix}+\begin{bmatrix}a_{13}&a_{14}\\a_{23}&a_{24}\end{bmatrix}\begin{bmatrix}b_{31}&b_{32}\\b_{41}&b_{42}\end{bmatrix}$

Таким же чудесным образом можно разбить матрицу 16×16, 256×256, и вообще любую квадратную матрицу с количеством строк/столбцов равным степени двойки.

Зачем это делать, спросит вдумчивый читатель?

Допустим у вас есть метод, который очень быстро умножает матрицы 4×4 (есть такие операции в NEON, SIMD и прочих MMX) и вам надо ускорить умножение огромной матрицы 32×32.

Воспользуйтесь кодом из лекции MIT (смотреть с 44-й минуты):

и вызывайте вместо

C[0] += A[0] * B[0];

свой метод, а вместо проверки (n == 1) поставьте (n == 4). Кстати, количество умножений в этом случае будет равно 512, а поэлементно — 32768. Почувствуйте разницу!

Оптимизированная версия кода из лекции MIT:

public void Rec_Mult(double[] C, int offC, double[] A, int offA, double[] B, int offB, int n, int rowsize) {
    if (n == 1) {
        C[offC] += A[offA] * B[offB];
    }
    else {
        final int d11 = 0;
        final int d12 = n / 2;
        final int d21 = (n / 2) * rowsize;
        final int d22 = (n / 2) * (rowsize + 1);
 
        final int C11 = offC + d11;
        final int A11 = offA + d11;
        final int B11 = offB + d11;
 
        final int C12 = offC + d12;
        final int A12 = offA + d12;
        final int B12 = offB + d12;
 
        final int C21 = offC + d21;
        final int A21 = offA + d21;
        final int B21 = offB + d21;
 
        final int C22 = offC + d22;
        final int A22 = offA + d22;
        final int B22 = offB + d22;
 
        // C11 += A11 * B11
        Rec_Mult(C, C11, A, A11, B, B11, n / 2, rowsize);
        // C11 += A12 * B21
        Rec_Mult(C, C11, A, A12, B, B21, n / 2, rowsize);
 
        // C12 += A11 * B12
        Rec_Mult(C, C12, A, A11, B, B12, n / 2, rowsize);
        // C12 += A12 * B22
        Rec_Mult(C, C12, A, A12, B, B22, n / 2, rowsize);
 
        // C21 += A21 * B11
        Rec_Mult(C, C21, A, A21, B, B11, n / 2, rowsize);
        // C21 += A22 * B21
        Rec_Mult(C, C21, A, A22, B, B21, n / 2, rowsize);
 
        // C22 += A21 * B12
        Rec_Mult(C, C22, A, A21, B, B12, n / 2, rowsize);
        // C22 += A22 * B22
        Rec_Mult(C, C22, A, A22, B, B22, n / 2, rowsize);
    }
}

Пример работы на C/C++ для (n == 2)

#include <stdio.h>
#include <string.h>
 
 
void Rec_Mult(int *C, const int *A, const int *B, int n, int rowsize)
{
    if (n == 2)
    {
        const int d11 = 0;
        const int d12 = 1;
        const int d21 = rowsize;
        const int d22 = rowsize + 1;
 
        C[d11] += A[d11] * B[d11] + A[d12] * B[d21];
        C[d12] += A[d11] * B[d12] + A[d12] * B[d22];
        C[d21] += A[d21] * B[d11] + A[d22] * B[d21];
        C[d22] += A[d21] * B[d12] + A[d22] * B[d22];
    }
    else
    {
        const int d11 = 0;
        const int d12 = n / 2;
        const int d21 = (n / 2) * rowsize;
        const int d22 = (n / 2) * (rowsize + 1);
 
        // C11 += A11 * B11
        Rec_Mult(C + d11, A + d11, B + d11, n / 2, rowsize);
        // C11 += A12 * B21
        Rec_Mult(C + d11, A + d12, B + d21, n / 2, rowsize);
 
        // C12 += A11 * B12
        Rec_Mult(C + d12, A + d11, B + d12, n / 2, rowsize);
        // C12 += A12 * B22
        Rec_Mult(C + d12, A + d12, B + d22, n / 2, rowsize);
 
        // C21 += A21 * B11
        Rec_Mult(C + d21, A + d21, B + d11, n / 2, rowsize);
        // C21 += A22 * B21
        Rec_Mult(C + d21, A + d22, B + d21, n / 2, rowsize);
 
        // C22 += A21 * B12
        Rec_Mult(C + d22, A + d21, B + d12, n / 2, rowsize);
        // C22 += A22 * B22
        Rec_Mult(C + d22, A + d22, B + d22, n / 2, rowsize);
    }
}
 
 
#define ROW_COUNT 8
 
 
void printMatrix(const char *name, const int *mat)
{
    printf("%s:\n", name);
 
    for (int i = 0; i < ROW_COUNT; ++i)
    {
        for (int j = 0; j < ROW_COUNT; ++j)
        {
            printf("%4d", mat[i * ROW_COUNT + j]);
        }
        printf("\n");
    }
    printf("\n");
}
 
 
int main()
{
    const int matA[ROW_COUNT * ROW_COUNT] =
    {
        1, 2, 3, 0, 0, 4, 5, 6,
        1, 2, 3, 0, 0, 4, 5, 6,
        1, 2, 3, 0, 0, 4, 5, 6,
        1, 2, 3, 0, 0, 4, 5, 6,
        1, 2, 3, 0, 0, 4, 5, 6,
        1, 2, 3, 0, 0, 4, 5, 6,
        1, 2, 3, 0, 0, 4, 5, 6,
        1, 2, 3, 1, 1, 4, 5, 6,
    };
 
    const int matB[ROW_COUNT * ROW_COUNT] =
    {
        2, 2, 2, 2, 2, 2, 2, 2,
        3, 3, 3, 3, 3, 3, 3, 3,
        0, 0, 0, 0, 0, 0, 0, 0,
        4, 0, 0, 0, 0, 0, 0, 2,
        4, 0, 0, 0, 0, 0, 0, 2,
        0, 0, 0, 0, 0, 0, 0, 0,
        0, 0, 0, 0, 0, 0, 0, 0,
        1, 1, 1, 1, 1, 1, 1, 1,
    };
 
    int matC[ROW_COUNT * ROW_COUNT];
    memset(matC, 0, sizeof(matC));
 
    Rec_Mult(matC, matA, matB, ROW_COUNT, ROW_COUNT);
 
    printMatrix("Matrix A", matA);
    printMatrix("Matrix B", matB);
    printMatrix("Multiply", matC);
 
    return 0;
}

#include <stdio.h> #include <string.h> void Rec_Mult(int *C, const int *A, const int *B, int n, int rowsize) { if (n == 2) { const int d11 = 0; const int d12 = 1; const int d21 = rowsize; const int d22 = rowsize + 1; C[d11] += A[d11] * B[d11] + A[d12] * B[d21]; C[d12] += A[d11] * B[d12] + A[d12] * B[d22]; C[d21] += A[d21] * B[d11] + A[d22] * B[d21]; C[d22] += A[d21] * B[d12] + A[d22] * B[d22]; } else { const int d11 = 0; const int d12 = n / 2; const int d21 = (n / 2) * rowsize; const int d22 = (n / 2) * (rowsize + 1); // C11 += A11 * B11 Rec_Mult(C + d11, A + d11, B + d11, n / 2, rowsize); // C11 += A12 * B21 Rec_Mult(C + d11, A + d12, B + d21, n / 2, rowsize); // C12 += A11 * B12 Rec_Mult(C + d12, A + d11, B + d12, n / 2, rowsize); // C12 += A12 * B22 Rec_Mult(C + d12, A + d12, B + d22, n / 2, rowsize); // C21 += A21 * B11 Rec_Mult(C + d21, A + d21, B + d11, n / 2, rowsize); // C21 += A22 * B21 Rec_Mult(C + d21, A + d22, B + d21, n / 2, rowsize); // C22 += A21 * B12 Rec_Mult(C + d22, A + d21, B + d12, n / 2, rowsize); // C22 += A22 * B22 Rec_Mult(C + d22, A + d22, B + d22, n / 2, rowsize); } } #define ROW_COUNT 8 void printMatrix(const char *name, const int *mat) { printf("%s:\n", name); for (int i = 0; i < ROW_COUNT; ++i) { for (int j = 0; j < ROW_COUNT; ++j) { printf("%4d", mat[i * ROW_COUNT + j]); } printf("\n"); } printf("\n"); } int main() { const int matA[ROW_COUNT * ROW_COUNT] = { 1, 2, 3, 0, 0, 4, 5, 6, 1, 2, 3, 0, 0, 4, 5, 6, 1, 2, 3, 0, 0, 4, 5, 6, 1, 2, 3, 0, 0, 4, 5, 6, 1, 2, 3, 0, 0, 4, 5, 6, 1, 2, 3, 0, 0, 4, 5, 6, 1, 2, 3, 0, 0, 4, 5, 6, 1, 2, 3, 1, 1, 4, 5, 6, }; const int matB[ROW_COUNT * ROW_COUNT] = { 2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3, 0, 0, 0, 0, 0, 0, 0, 0, 4, 0, 0, 0, 0, 0, 0, 2, 4, 0, 0, 0, 0, 0, 0, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, }; int matC[ROW_COUNT * ROW_COUNT]; memset(matC, 0, sizeof(matC)); Rec_Mult(matC, matA, matB, ROW_COUNT, ROW_COUNT); printMatrix("Matrix A", matA); printMatrix("Matrix B", matB); printMatrix("Multiply", matC); return 0; }

Если немножко изменить код, то можно умножать неквадратные матрицы, но с шириной/высотой равной степени двойки (например, 16×4 на 4×16).

В принципе, блочный способ умножения можно применять к любым матрицам, просто разложение на блоки будет сложнее.

И напоследок — в процессе поиска информации по этому методу не нашел НИ ОДНОГО сайта на русском языке, который объяснял бы подобный метод для профанов. Одни только хвалебные оды самому себе в стиле: «реализовал блочное умножение матриц, алгоритм и реализацию ищите сами, у меня теперь все стало быстрее». Молодцы, так держать! Зачем делиться информацией, правда, ведь, да?