Устройство движка для квестов Trickster Games

28 марта 2025 33 #c++#python #trickster games #полезная статья

Всем привет! В результате недавних трудов у меня появились исходники движка для квестов компании Trickster Games. Выкладывать я их не буду, потому что не знаю насколько он лицензионно чистый. Я не юрист, в таких вопросах не разбираюсь. Поэтому расскажу своими словами — как устроен движок для квестов Trickster Games.

Поколений движков было два — первый использовался для игр Танита. Морское Приключение, Приключения Барона Мюнхгаузена на Луне и использовал lua в качестве скриптового языка.

Танита. Морское приключение и Приключения Барона Мюнхгаузена на Луне

Начиная с игры «Петрович и все, все, все» движок переходит на использование Python 2.xx вместо lua. Я пришёл в Trickster Games, когда начали делать Петрович, так что про предыдущие движки и игры практически ничего не знаю.

Итак, приступим!

Описание редактора игрового движка Trickster Games

Небольшое отступление: движок казался гораздо проще. Однако, он содержит в себе множество разных python классов, буду заново разбираться по ходу написания статьи.

Итак, у нас есть редактор (это первый уровень игры «Петрович и все все все»):

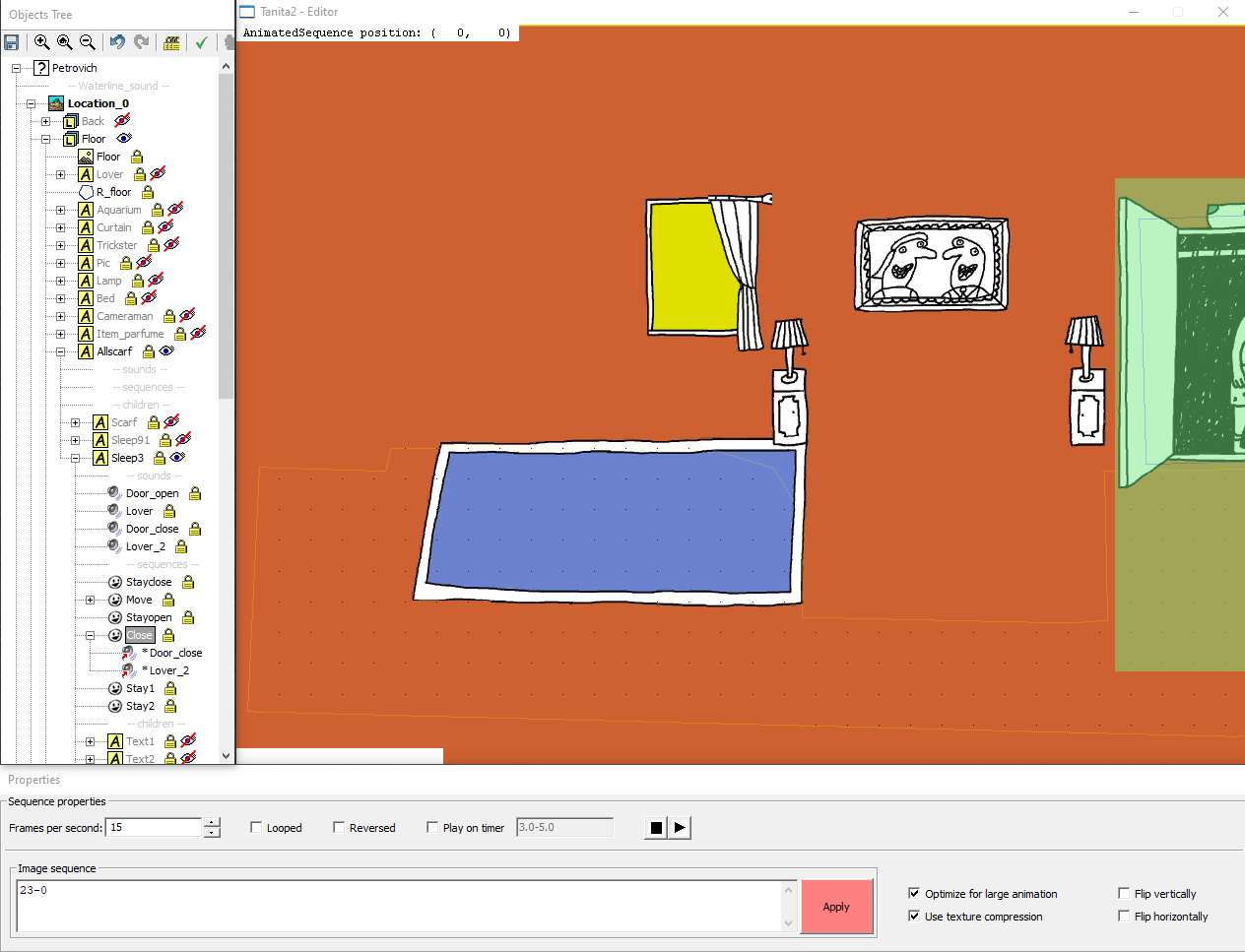
Редактор Trickster Games

Это тот же самый движок, но запущенный в специальном режиме.
Слева у нас окно дерева объектов, снизу свойства объекта, а справа самый большой экран — экран предпросмотра уровня. Фон заполняется жёлтым цветом, чтобы на сцене сразу были видны пустые места. В режиме игры, фон заполняется чёрным цветом, так что это не бросается в глаза в обычном режиме.

Почти все объекты наследуются от ItemBase и рисуются относительно координат родителя. При перемещении родительского элемента на сцене, его дети перемещаются вместе с ним. В дереве объектов элементы можно перетаскивать с помощью drag-n-drop или добавлять новые правой кнопкой мыши. У каждого элемента есть замочек и глазик — блокировать перемещение/выделение при клике на сцену и показать/спрятать элемент при отрисовке сцены. Отрисовка элементов идёт по дереву от корневого узла вниз.

Уровень (Location)

Собственно уровень игры, рутовый элемент нашей сцены, содержит параметры width, height — ширина локации, высота локации. Вот её панель свойств:

Свойства локации в игровом редакторе Trickster Games

Может содержать в качестве детей только слои.

Слой (Layer)

Слой локации, имеет параметр parallax — это отставание при прокрутке. С помощью него создаётся эффект глубины при скроллинге локации по горизонтали или вертикали. Вот её панель свойств:
Свойства слоя в игровом редакторе Trickster Games Может содержать в качестве детей статические изображения, регионы, пути, анимированные объекты и точки.

Статическое изображение (LayerImage)

Фоновое изображение, ничего не делает, просто рисуется с соответствующим свойствами (параллакс) слоя. Имеет довольно скудный набор свойств:

Свойства статического изображения в игровом редакторе Trickster Games

Анимированный объект (AnimatedObject)

Можно сказать, что это наш главный элемент, базовый кирпичик нашего движка. У него есть позиция, набор состояний, к нему привязываются звуки, регионы, а также скрипт.

Свойства игрового объекта в игровом редакторе Trickster Games

Он может наследоваться от особенных классов, например, Playable Character — это наш главный герой, который умеет ходить по локации, или Takeable Item — это вещь, которую можно забрать себе в инвентарь. Он может загружаться согласно определённым условиям из скрипта, если поставить флажок «Conditional object loading». Пример условной загрузки элемента «Item_parfume» (условия описываются в родительском элементе):

class FloorLayer:
    def should_load_Item_parfume(self):
        return not world.parfume_taken

Также у него есть pivot — начало его координат и позиция на локации абсолютная и относительная. К нему могут привязываться дочерние AnimatedObject, Region и StateSequence. Содержит список состояний. Представляет собой конечный автомат, который меняет своё состояние в зависимости от внешних условий. Может загружать дочерние элементы типа AnimatedObject по некоторым условиям.

Состояние объекта (AnimatedSequence)

Анимация и состояние AnimatedObject. Анимация неотделима от состояния объекта. Пока AnimatedObject находится в определённом состоянии, проигрывается анимация этого состояния из одного или нескольких кадров. К любому кадру можно привязать автоматическое проигрывание звука.
Свойства состояния объекта в игровом редакторе Trickster Games

У состояния есть свойства on_enter, on_exit, link, on_update — для привязки пользовательских функций. on_enter выполнятся при переходе в это состояние, on_exit — при выходе из него, link — выполняется каждый кадр, и если возвращает строку, то состояние меняется на указанное, on_update вызывается каждым кадр с неким dt (количество миллисекунд между кадрами).

Регион (Region)

Некий замкнутый набор точек. Определяет область для хождения главного героя на сцене (на скриншоте редактора это R_Floor) и области для клика мышкой. Имеет свойство
«.click» или «.click_with_» для проверки клика на этот регион, второе свойство динамическое и проверяется клик с предметом из трея. Предоставляет метод для поиска кратчайшего пути между точками для хождения главного героя. Может иметь несколько типов (не помню, кто за что отвечает) и менять курсор мыши при наведении.
Свойства региона в игровом редакторе Trickster Games

Путь (Path)

Путь состоящий из нескольких точек. Можно привязать элемент к этому пути, и объект будет плавно по нему перемещаться.
Свойства пути в игровом редакторе Trickster Games

Точка (Point)

Точка на уровне. В основном используется, чтобы указывать, куда подходит главный герой для выполнения действий. Настраиваемых свойств в редакторе не имеет, только позицию.

Описание игрового движка Trickster Games

Движок написан на C++, для рендера используется DirectX 9.0, для связки Python 2.xx и C++ используется Boost.Python. Для сборки и компиляции исходников движка применяется (БУДЬТЕ ПРОКЛЯТЫ ЕГО СОЗДАТЕЛИ!) Boost Jam и Visual Studio 2007.

Базовый элемент в игровом движке — это GameObject, который имеет матрицу трансформации себя относительно родителя, список детей типа GameObject, и используется для создания дерева сцены. Простыми словами, для отрисовки дерева сцены вызывается GameObject::update(dt), который последовательно вызывает обновления всех детей, начиная от корня дерева вниз по иерархии. От него торчат уши в Python. Python-часть движка инициализируется следующим кодом:

std::string setup(
"sys.path = [r'Data\Scripts1.pak', r'Data\Scripts2.pak', "
                    "r'Data\Scripts3.pak', r'Data\Scripts3.pak\CommonClasses', "
                    "r'Data\Scripts4.pak', r'Data\Scripts4.pak\World', '.', 'Lib/std']n");
run_string(setup);

Затем вызываем метод on_init из файла Lib/engine.py:

boost::python::call<void>(bp::object(py["Lib"].attr("engine").attr("on_init")).ptr(), long(application::Application::window()));
py_on_frame = py["Lib"].attr("engine").attr("on_frame");

И после делаем on_frame из того же файла каждый кадр:

boost::python::call<void>(py_on_frame.ptr(), dt / 1000.0f, just_redraw, cursor_position, mouse_button_state);

Всё, никакой магии.

Форматы файлов

При подготовке релиза происходит преобразование .py файлов в .pyc, PNG в DDS, и всё это запаковывается в .zip файл.

Анимация

Анимация делалась в Adobe Flash и экспортировалась в набор PNG файлов, которые при запаковке релиза превращаются в DDS — это родной формат для DirectX SDK.

Звуки

Звуки — это .wav файлы

Видео

Для видео использовался формат OGV (Theora Vorbis).

Вроде всё, что мог, описал. Спрашивайте, если что-то осталось непонятным.

Установка Python в режиме portable под Windows

17 марта 2016 3K #python

Установка Python

Скачать инсталлятор в формате MSI отсюда: https://python.org/downloads/
Установить полученный дистрибутив <python.msi> в папку <INSTALLDIR> командой:
```
msiexec /a <python.msi> /qn TARGETDIR="<INSTALLDIR>"
```
, где /a — команда на установку с админскими правами, /qn — не задавать лишних вопросов, TARGETDIR — конечная папка

Установка Python Package Index

Скачать файл getpip.py: https://bootstrap.pypa.io/get-pip.py
Установить pip командой:
```
python getpip.py
```
Теперь любые пакеты можно устанавливать командой:
```
python pip install [package_name]
```

В итоге у вас есть обособленный Python интерпретатор любой версии с любыми пакетами в комплекте.

Также у вас есть возможность запускать *.py файлы с помощью установленного дистрибутива по клику мыши. Для этого вам понадобится PyLauncher.

Установка и настройка PyLauncher

Скачать и установить pylauncer отсюда: https://bitbucket.org/vinay.sajip/pylauncher/downloads
Открыть/создать файл %LOCALAPPDATA%\py.ini и добавить строку:
```
[commands]
mypython=<INSTALLDIR>\python.exe
```
Добавить/поменять первую строку запускаемых *.py файлов на такую:
```
#!mypython
```
Теперь при запуске этих файлов их будет обрабатывать ваш интерпретатор

Как это работает?

Первая строчка в формате #!<program name> используется в *nix подобных системах для автоматического выбора интерпретатора во время запуска и называется она, кстати, «shebang». В Windows системах эта строка игнорируется. PyLauncher просто перехватывает обработку *.py файлов и вызывает правильный Python интерпретатор.

Ускорение работы Python

Я рекомендую отключать создание и обновление *.pyc и *.pyo файлов в процессе работы Python. Аргументы могу привести следующие: оперативной памяти сейчас у всех хватает, процессор достаточно быстрый. Но устройство хранения данных (в народе флешка, жёсткий диск, SSD) по-прежнему слабовато.

Поэтому не выпендривайтесь и запускайте python с параметром -B или добавьте параметр PYTHONDONTWRITEBYTECODE в переменную окружения с любым непустым значением. Например, PYTHONDONTWRITEBYTECODE=Non_empty_string.

Практическое применение B-сплайна (B-Spline) в программировании

4 сентября 2014 2K #python #линейная интерполяция #математика #формулы

Полтора дня разбирался в работе B-сплайна и как это применяется на практике. Хочу поделиться с вами результатами моих изысканий.

Немного теории

Допустим, у вас есть некий массив точек размером $n$ . Что вам потребуется для работы B-сплайна:

определить количество интерполируемых точек (от этого зависит скорость работы, гладкость получившейся кривой и размер формулы для вычисления, количество точек равно $k+1$ )
избавится от рекурсии формулы для вычисления

Общая формула для расчета коэффициентов:
$N_{i,k}(x)=\frac{x-t_i}{t_{i+k-1}-t_i}N_{i,k-1}(x)+\frac{t_{i+k}-x}{t_{i+k}-t_{i+1}}N_{i+1,k-1}(x)$

Формула рекурсивная и заканчивается на $k$ равном единице:
$N_{i,1}(x)=\begin{cases}1&\text{if }t_i\leq x\text{\textless} t_{i+1}\\0&\mathrm{otherwise}\quad\end{cases}$

Пояснения к формуле:

если делитель получается равным или близким по значению к нулю, значит вся дробь равна нулю
параметр $i$ — это индекс текущей точки
$x$ — значение от $i$ до $i + 1$ с нужным вам шагом (например, $i$ равно 7, и нам нужно создать 3 точки для интерполяции, значит берем $x$ равным 7.0, 7.5, 8.0)
$t$ — неубывающий массив индексов

Вычисление элементов массива $t$ :
$t=\begin{cases}0,&\mathrm{if}\ i<k\\i-k+1,&\mathrm{if}\ k\leq{i}\leq{n}\\n-k+2,&\mathrm{if}\ i>n\end{cases}$

Практика

Мне нужно было интерполировать по четырем точкам, поэтому я заранее на бумажке вычислил формулу без рекурсии:

N_{i,3}(x)=\begin{cases}0,&\mathrm{if}\ x\text{\textless} t_{i}\\\frac{x-t_i}{t_{i+2}-t_i}*\frac{x-ti}{t_{i+1}-ti},&\mathrm{if}\ t_i\leq x\text{\textless} t_{i+1}\\\frac{x-ti}{t_{i+2}-ti}*\frac{t_{i+2}-x}{t_{i+2}-t_{i+1}}+\frac{t_{i+3}-x}{t_{i+3}-t_{i+1}}*\frac{x-ti}{t_{i+2}-t_{i+1}},&\mathrm{if}\ t_{i+1}\leq x\text{\textless} t_{i+2}\\\frac{t_{i+3}-x}{t_{i+3}-t_{i+1}}*\frac{t_{i+3}-x}{t_{i+3}-t_{i+2}},&\mathrm{if}\ t_{i+2}\leq x\text{\textless} t_{i+3}\\0,&\mathrm{if}\ x\geq t_{i+3}\end{cases}

Про бумажку я, конечно, соврал, мне было удобнее сделать функцию на питоне вот такого вида:

def div(a, b):
    try:
        return a / float(b)
    except ZeroDivisionError:
        return 0

def N(i, k, x, t):
    if 1 == k:
        if t[i] <= x < t[i + 1]:
            return 1.0
        return 0.0
    a = div(x - t[i], t[i + k - 1] - t[i]) * N(i, k - 1, x, t)
    b = div(t[i + k] - x, x[i + k] - x[i + 1]) * N(i + 1, k - 1, x, t)
    return a + b

После этого добавил условие $k==2$ и все возможные возвращаемые значения в зависимости от $x$ , затем условие $k==3$ , значения которого зависят от $k==2$ . Может вам будет удобнее все это сделать на бумажке.

Наконец можно приступать к интерполяции. Формула такая: $\sum\limits_{i}^{i+k}=\vec{p_{i}}N_{i,k}(x)$

Если индекс точки меньше нуля, берем нулевую точку, если индекс точки больше размера массива, то берем последнюю точку в массиве.

Небольшой пример

У нас есть некий массив точек, нам надо интерполировать с пятой по шестую точки с шагом 0.25, при этом $k$ равно 3 (значит для интерполяции нужно взять четыре точки).

p_0=p_5*N_{0,3}(0.0)+p_6*N_{1,3}(0.0)+p_7*N_{2,3}(0.0)+p_8*N_{3,3}(0.0)\newline

p_1=p_5*N_{0,3}(0.25)+p_6*N_{1,3}(0.25)+p_7*N_{2,3}(0.25)+p_8*N_{3,3}(0.25)\newline

p_2=p_5*N_{0,3}(0.5)+p_6*N_{1,3}(0.5)+p_7*N_{2,3}(0.5)+p_8*N_{3,3}(0.5)\newline

p_3=p_5*N_{0,3}(1.0)+p_6*N_{1,3}(1.0)+p_7*N_{2,3}(1.0)+p_8*N_{3,3}(1.0)\newline

Итого четыре новых точки вместо двух.

Спасибо за внимание, надеюсь нигде не ошибся. На несложные вопросы по теме могу ответить в комментариях.

Извлекаем вектор и угол из матрицы поворота

26 февраля 2013 2K #python #вектор #математика #матрица #формулы

В продолжение темы кватерниона…

Итак, есть матрица 4×4, где три оси ортогональны друг другу (по-нашенски, по-деревенски — это означает, что три оси перпендикулярны каждая с каждой, представьте оси прямоугольной системы координат, так вот это оно и есть).

Выглядит матрица вот так:

M=\begin{bmatrix}A&E&I&M\\B&F&J&N\\C&G&K&O\\D&H&L&P\end{bmatrix}

В ней, как я уже рассказывал, «живут» три вектора ABC (ось X), EFG (ось Y), IJK (ось Z). Также есть три смещения вдоль XYZ — это M, N и O соответственно.

Для того, чтобы извлечь вектор и угол из этой матрицы я использую вот такую конструкцию (псевдокод):

def getAngleAxis(m):
    xx = m[A]
    yy = m[F]
    zz = m[K]

    # Сумма элементов главной диагонали
    traceR = xx + yy + zz

    # Угол поворота
    theta = acos((traceR - 1) * 0.5)

    # Упростим вычисление каждого элемента вектора
    omegaPreCalc = 1.0 / (2 * sin(theta))

    # Вычисляем вектор
    w.x = omegaPreCalc * (m[J] - m[G])
    w.y = omegaPreCalc * (m[C] - m[I])
    w.z = omegaPreCalc * (m[E] - m[B])

    # Получаем угол поворота и ось, 
    # относительно которой был поворот
    return (theta, w)

Мне довелось применять этот метод на матрице, где вектора ABC, EFG и IJK нормализованы. Масштаб хранится отдельно. Если вы храните масштаб внутри матрицы, то перед применением формулы надо нормализовать вектора ABC, EFG и IJK).

Убираем резкие перепады входных данных

5 февраля 2013 23 #python #линейная интерполяция #математика #формулы

И снова в эфире наша рубрика: «Банальности программирования в массы»…

В этот раз хочу поделиться с народом штукой под названием «Low-pass filter».

«Ну что ты, в самом деле, опять про то, что все уже давным-давно знают» — скажут опытные программисты. «А вот ничего подобного» — отвечу им, лично я узнал об этом совсем недавно. И очень жалею, что не знал этого раньше.

Итак, вот функция для сглаживания входных данных:

def filter(a, b, dt, RC):
    t = dt / (RC + dt)
    return a + t * (b - a)

где a — текущее значение переменной, b — следующее значение, dt — время в миллисекундах между кадрами, RC — некий коэффициент (чем больше значение, тем больше сглаживание).

Соответственно, если вам надо сгладить какое-то значение (например, позицию камеры по Y в зависимости от позиции Y главного героя), то можно применить эту функцию следующим образом (значение RC подбирается опытным путем):

def update(dt):
    camPosY = filter(camPosY, heroPosY, dt, 0.85)

Кстати, тут используется линейная интерполяция, которая вкратце описана в этой заметке: «Линейная интерполяция и кривая Безье».

Список постов с меткой "Python"